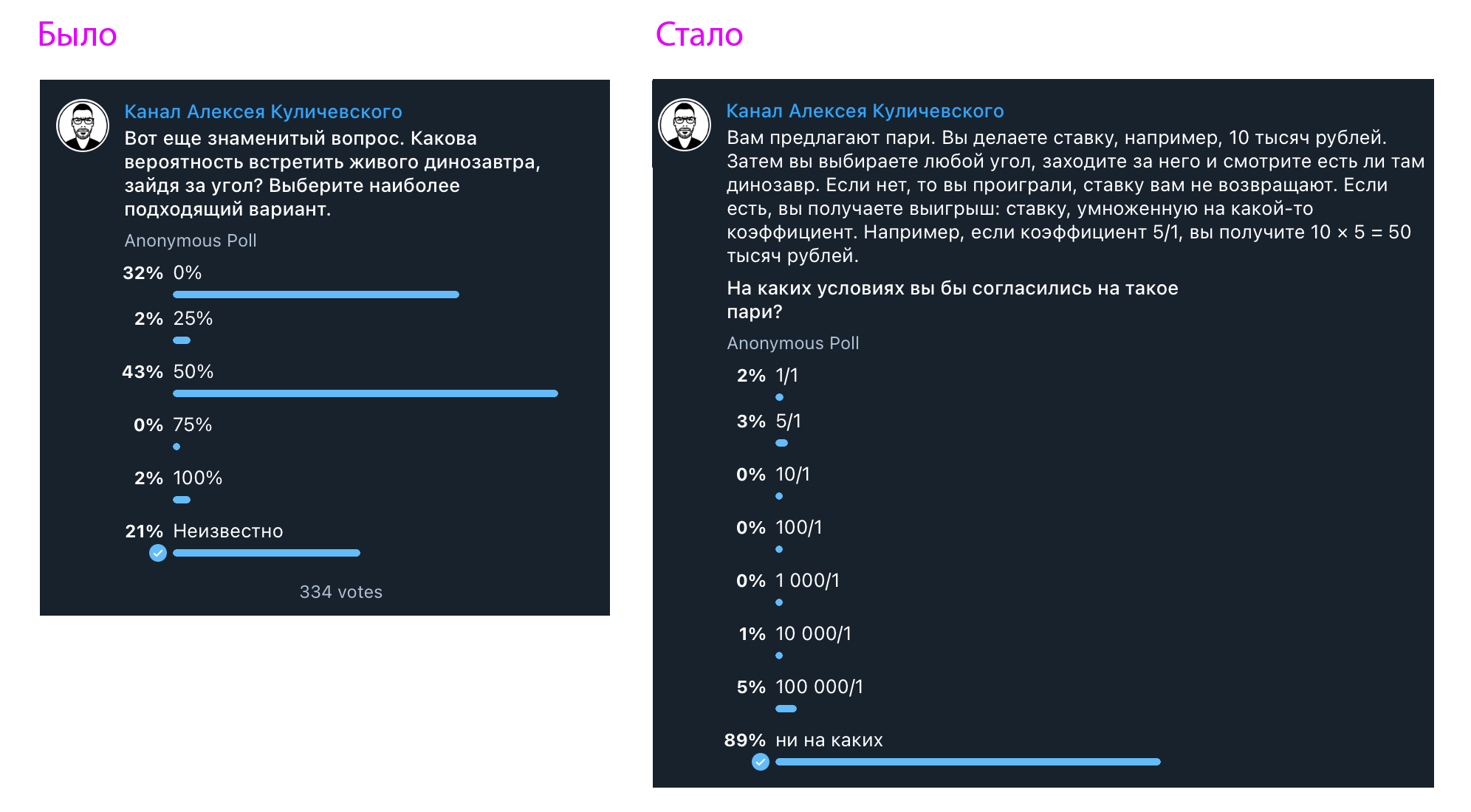
Какова вероятность встретить динозавра за углом? 🦖
Есть старый анекдот:
Блондинку спрашивают:
— Если ты зайдешь за угол, какова вероятность того, ты там встретишь динозавра?
— 50%. Либо встречу, либо нет.
Юмор в том, что, с одной стороны, блондинка дает наивный и абсурдный ответ. Но с другой стороны без погружение в теорию вероятностей сходу найти ошибку в рассуждениях может не получиться. Ведь правда, либо встретит, либо нет.
В прошлой заметке я рассказал про случайные события, случайные величины, пространства вариантов и про то, что вероятность — это свойство конкретного значения случайной величины.
Теперь давайте разберемся, что это за свойство такое, как его измерять. И, наконец, разберемся с динозаврами.
Для наглядности решим простую задачу.
Простая задача
🎲 Задача: какова вероятность получить четное число, если подбросить игральный кубик?
Обычно в учебниках вероятность объясняется на примерах из азартных игр: подбрасываниях монеты или игральных кубиков, доставания наугад цветных шариков из мешка. Это позволяет упростить понимание, не теряя при этом нужных деталей. А раз так, то не будем придумывать велосипед, и некоторое время поподбрасываем кубики.
Распакуем задачу в известные нам понятия:
Cлучайное событие — подбрасывание кубика. Мы заранее не знаем, какое число мы получим.
Случайная величина — полученное в результате подбрасывания число.
Предположим, что у нашего кубика 6 граней. То есть пространство вариантов случайной величины: целые числа 1, 2, 3, 4, 5, 6.
В основе теории вероятностей лежит «классическое» определение вероятности.
ℹ️ Вероятность события A равна отношению количества равновозможных элементарных событий, составляющих событие А к числу всех возможных элементарных событий.
Формула: P(A) = m/n
P(A) — вероятность события A
m — количество равновозможных событий, входящих в, А
n — общее количество возможных событий
В определении встречаются несколько неизвестных нам фраз. Переведем их на русский.
Так для краткости называют какое-то целевое событие, вероятность которого мы хотим посчитать. Например, в этой задаче «Событие А» — получение четного числа.
Элементарным событием называют выпадение любого значения из пространства вариантов. Например, выпадение 1, 2 или 5.
Целевое событие может состоять из какой-то комбинации элементарных событий. Например, выпадение четного числа означает выпадение 2, 4 или 6.
Обычный игральный кубик может с равной вероятностью упасть любой стороной вверх. То есть возможность получить единицу, двойку и т. п. одинаковы. Или, другими словами, все исходы одного броска кубика равновозможны.
Окей, вроде, все определения есть. Теперь сформулируем решение задачи через классическое определение вероятности и решим ее.
Вероятность выпадения четного числа при подбрасывании игральной кости.
…равна отношению количества равновозможных элементарных событий, составляющих событие А…
Равновозможные элементарные события, составляющие выпадение четного числа: выпадение 2, 4, 6.
Всего таких событий 3.
…к числу всех возможных элементарных событий.
Все элементарные события из пространства вариантов: 1, 2, 3, 4, 5, 6. Всего их 6.
Итого, вероятность P(четное число) = 3/6 = ½ = 50%
Вернемся к задаче про динозавра 🦖.
Как раз из классического определения вероятностей следует предложенное блондинкой решение про 50%.
Событие А — заходим за угол. Элементарных событий два: либо встречаем динозавра, либо нет. Удовлетворяет условию только одно. Значит итоговая вероятность P(встретить динозавра) = ½ = 50%.
Но теперь лучше видно, что мы упустили важное условие про равновозможность вариантов. Чтобы разобраться, решим еще одну задачу с кубиками, теперь посложнее.
Задача посложнее
🎲 Задача: какова вероятность получить число, от 6 и до 10 при броске двух игральных кубиков?
Побудем занудами и прежде, чем прыгать к решению, распакуем задачу в известные понятия. Поверьте, это хорошая практика.
В этой задаче случайное событие — подбрасывание двух игральных кубиков.
Тут без изменений. Случайная величина — полученное в результате подбрасывания число.
Мы подбрасываем два кубика. Каждый может принять значения от 1 до 6. То есть совместно они могут дать от 2 до 12.
Получение числа от 6 и до 10.
А вот тут интересно. Когда мы подбрасывали один кубик, мы могли получить каждое значение только одним способом. Например, чтобы получить 3, нужно было, чтобы кубик упал тройкой наверх.
Теперь мы бросаем два кубика и можем получить тройку, если на первом кубике выпадет 1, а на втором 2, или если на первом выпадет 1, а на втором 2.
То есть в этой задаче элементарное событие — не итоговое количество выпавших очков, а выпадение комбинации цифр на двух кубиках.
Некоторые числа из пространства вариантов можно получить только одним способом. Например, чтобы получить двойку, нужно, чтобы на обоих кубиках выпали единички. А другие числа можно получить несколькими способами. Я выше описал способы получить число тройку. Считать выпадение двойки и тройки равновозможными — ошибка.
Но вот выпадение каждой комбинации из двух кубиков все еще равновозможна. Выпадение 1 и 4 случается с такой же частотой, как и выпадение 4 и 1 или 3 и 2.
Теперь сформулируем решение задачи через классическое определение вероятности.
Вероятность выпадения числа от 6 и до 10 при бросании двух игральных кубиков.
…равна отношению количества равновозможных элементарных событий, составляющих событие А…
Выпадение 6, 7, 8, 9, 10.
Шестерка может выпасть пятью способами: 1+5, 2+4, 3+3, 4+2, 5+1. Семерка — шестью способами.
Всего нужные нам числа попадаются 23 раза.
…к числу всех возможных элементарных событий.
Все элементарные события из пространства вариантов: 1+1, 1+2, 1+3 и так далее. Всего элементарных событий в данном случае 36.
Итого, вероятность P(от 6 до 10) = 23/36 ≈ 63.9%.
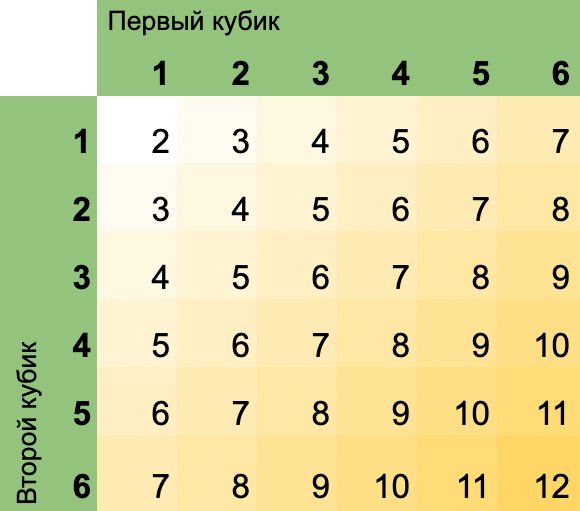
Всего возможны 36 вариантов результата подбрасывания двух игральных кубиков.
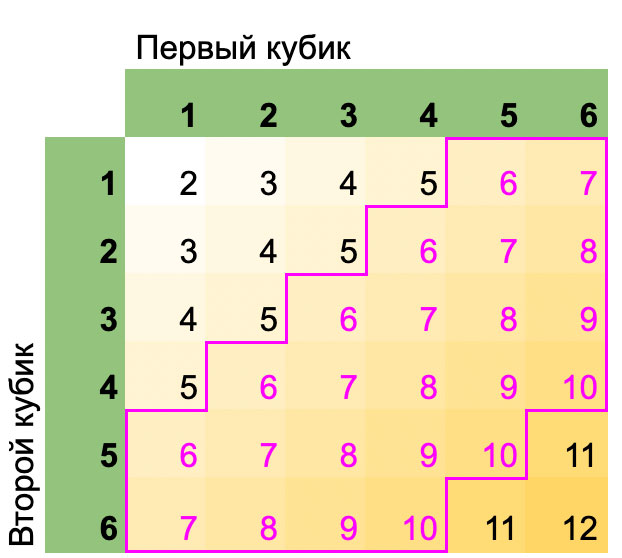
Из всех вариантов нам подходят 23.
В принципе, при наличии данных, с помощью этого способа можно решить любую задачу на вероятность: cчитаем количество равновозможных элементарных событий, удовлетворяющих целевому событию, делим на общее их количество и вуаля — готово!
Но, сожалению, в реальной жизни нужных данных может не быть, и тогда приходится придумывать другие решения. Задача про динозавра как раз отлично подходит для иллюстрации этого ограничения. Давайте попробуем ее решить.
Задача про динозавра
🦖 Задача: какова вероятность, зайдя за угол, встретить динозавра?
Как обычно, распишем задачу на части.
Кого мы встретим за углом.
Вот тут начинаются проблемы. Зайдя за угол мы можем встретить динозавра, пришельца, Джастина Бибера, Ромку из 7 «Б», а можем и вообще никого не встретить. Пространство вариантов где-то между «поди разбери» и бесконечностью.
Тут тоже неясно. Нас интересует какой-то конкретный динозавр? Он обязательно должен быть живым? А надувной подойдет? Говорят, что птицы — тоже динозавры. Они считаются?
Тут просто. Заходим за угол и смотрим, кто там.
С равновозможностью вообще провал. Скорее всего, за углом никого. Может быть там кто-то есть. Но точно у всех возможных вариантов вероятность будет сильно отличаться.
Получается, что вероятность встретить динозавра за углом равна какому-то непонятному числу в числителе, деленному на еще более непонятное число в знаменателе.
К сожалению, решение «либо встречу, либо нет» из анекдота не подходит. К сожалению, ни при каких условиях варианты «динозавр» и «не динозавр» не могут быть равновозможными. Значит, классическое определение вероятности применять нельзя.
Более того, это значит, что, строго говоря, точное значение вероятности встретить динозавра неизвестно и никогда не будет известно. И похожая проблема распространяется практически на все события в реальном мире. Точно посчитать их вероятности невозможно потому что пространство вариантов у этих событий либо неопределено, либо бесконечно.
Но хорошая новость в том, что для принятия решений знать точную вероятность не обязательно. Достаточно прикинуть ее с какой-то комфортной погрешностью.
Например, интуитивно понятно, что за углом может быть кто угодно, пространство вариантов огромное и, вероятность встретить динозавра хоть и неизвестна, но, скорее всего, она где-то около нуля.
Забавно, что если сформулировать вопрос в своей изначальной форме, многие отвечают «50%». Но стоит чуть переформулировать вопрос, повысить ставки и добавить принятие решения, общественное мнение безошибочно смещается.
В следующей заметке мы поговорим о том, какие бывают способы оценивать вероятность событий в реальном мире. Подписывайтесь в Телеграме, обычно все анонсы пишу туда.
🔗 https://t.me/kulichevskiy